
��������� �������
�������� �������
���������� ������� y = f(x), ������� ��������������� �� ���������� (�, b).
���� ����� ������� ����� �-����������� ����� �1 ������������� ���������� (�, b), ��� ��� ���� � (�1, �), ����������� ����������� f(x1) > f(x), �� y1 = f1(x1) �������� ���������� ������� y = f{x) �� ���.
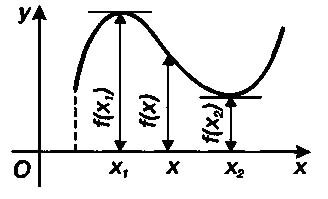
�������� ������� y = f{x) �������� ����� max f(x). ���� ����� ������� ����� �-����������� ����� �2 ������������� ���������� (�, b), ��� ��� ���� � ������������� � (�2, 6), � �� ����� �2 ����������� ����������� f(x2) < f(x), �� y2= f(�2) �������� ��������� ������� y-f{x) (��. ���.).
������ ���������� ��������� �������� �� ��������� �����
������� �������
������� ������� � = f(x) ��������� ����� min f(x). ������� �������, ���������� ��� ��������� ������� � = f(x) �������� ����� �� ��������, ������� ������ (������) ���� ������ ��������, ����������� � ������, ���������� ������� � ������ � �������� �� ���.
��������� 1. �������� �������, ������������ ������������ ���������� ������� ����������; ��������� �������� ������������ ������������ f(x1) > = f(x2)
��������� 2. �������� � ������� ������� ����� ��������� �������� (��� ���������� � ���������� �������� ������� � ���������� ����� ����������� ��������������� �����); ��������� �������� ��������� ������� ����� ��������� ������ ���������� ��� �� �������
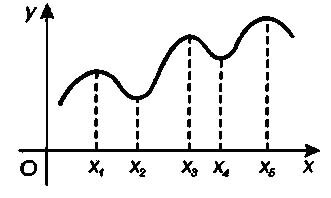
���������� ����� �������� (�������) ������� �������� ��������� ���������� (��������� ���������) � ������� �� ����������� ��������� (��������) - ����������� (�����������) �������� � ������� ����������� �������.
�������� � ������� ������� ���������� �����������. ���������� � ����������� �� ���������� ������� ��� ���������� �������� �������
��������� extremum �������� �������� ��������. �������� ��������� �, ��� ������� ����������� ���������, ���������� ������ ����������. ����������� ������� ���������� ���������� ��������� ��������.
�������. � ����� ���������� ���������������� ������� � �� ����������� ����� ����.
������� ����� ������� �������������� �����: ����������� � ������� ���������������� ������� � ��������������� ����� ����������� ��� ��


