��

�� , ��

�� y=f(x), �� [�, b], �� < b. �� [�, b] �� = �0 < �1 < �2 < ... < �n = b �� n �� [�, �1] , [�1, ,�2],...,[xn-1, b], �� k.

� �� [xk-1, xk] �� k �� k, �� . ��

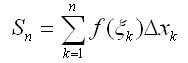
�� y = f(x) �� [�, b]. �� , �� [xk-1, xk] (k = 1,2,...,n), �.�. � = m�� k.

�� S �� S, �� > 0 �� > 0, �� < � �� |Sn - S| < e �� [xk-1, xk]

�� = f(x) �� [�, b] �� , �� , � �� . ��

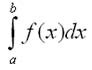
f(x) �� �� , � - �� , a - ��, b - �� . ��, ��

�� , �� , �.�.

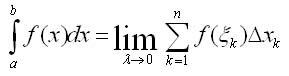
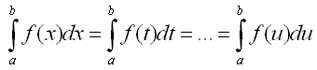
��, �� , �� [�, b].

��, �� -�� f(x) �� [�, b] �� . �� : �� , �� . � �� �� , �� - � ��. �� [�, b] �� , �� .

��

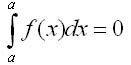
�� f(x) - �� ;

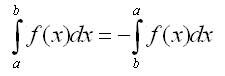
�� f(x) � ��, �� [b, a] (b < a). �� .

1. �� f(x) �� [�, b], �� [�, d], �� [�, b].

2. �� f(x) �� [�, b], �� .

3. �� f(x) �� [�, b] �� , �� [�, b].

������������ ��������