
������ ��������������
���������������� ��������������
���������������� �������������� �������� �� �������� 4 ��������������� ��������� ���� ������� f1(x), � fn(x) ����� ������������� � ��������� ����������, �� ������� f(x) = f1(x)+f2(x)+f3(x)+�+-fn(x) ����� ����� ������������� � ��� �� ����������, ������
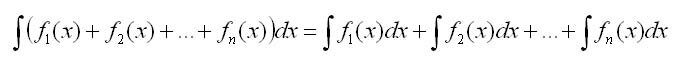
�.�. �������������� �������� �� ����� ���������� ����� ������� ����� ����� �� ����� �������������� ���������� �� ���������.
������� �����, �������� � ������� ����������������� ��������������, ��������������� �� ��������� �����
����� �����������
�������������� ������������ ��������� ����� ���������� (��� ����� �����������) �������� �� �������
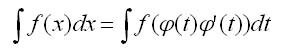
��� x = �(t) � ���������������� ������� ��������� t.
������, �������� � ������� ������ �����������, ��������������� �� ��������� �����
����� �������������� �� ������
���� u = u (�), v = v (�) - ���������������� ������� �� �, �� �� ������� ��� ������������� ������������ ���� ������� d(uv) = udv+vdu ���������� ������� �������������� �� ������
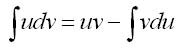
��� ������� ����������� � ������, ����� ��������������� ������� ������������ ����� ������������ �������������� � ��������������� �������. � �������� � ������ ���������� �������, ������� ���������� ������������������, � �������� dv � ���������� ����� ���������������� ���������, ���������� dx, �� ������� ����� ���������� v ����� ��������������.
��� �������� ������� ��������� � ����� �� ������ ���������� ���������� ������� ����� ��������� ��������� ���. ������ ������� �������� ������������ �� ��������������� ���������, ������������� � ������� �������������� �� ������.
�������� ������, �������� ������� �������������� �� ������, �� ��������� �����


