
������������, ���������� � �������� �������
������������ �������
������������ ������� ��������������� ���, ��� ����� ������ � ���������� ������������ �� �����������, �������� �� ������������ �������� �� ������ ���������, � ������� ���������� ���������� ���, ��� �� ������ ����� ������ � ������� ���������� ���� ���� �������.
��� ����, ����� �������� ��������������� ������, ���������� �������, ������� ��������� � �������� ������ ������.
��� ����������� ������������� ������ ������� ������������ ������� ����������� � ������������ ������� � ����� �������� �������� ����� ������ ����������� ����� ������������ ��������. ��� ���� ������ ��������� � ����������� ������������ ����� ��������� �������� ���� �������.
��� ������� ���������� ������� ������������ ������������ ����� �� �������� ����������� ������ � ����������. ������� ��� ����������� ������� ������ ������������ ������� ���������� ��������� ����������-��������� ������������ �������.
���������� �������
���������� ������� ��������� ��� ������ ������ �� ������������ ������������. ��� ������������ �����, ����� ��� ������� ����������� ������������ ����� ������� �� ��������� ����������� ���������� ����� �� ���������, ������� ������ �� ��������� ����������.
��� ������� ����������� ������ �������� ����� ����: �������, ����� �������������, ��������� ������ � �. �. ����� �� ������ ���������� ������ ������������ ��� ����������-��������� �������� ���������� �������������� ����� ������ � ���������� ������������.
����� ���������� ������� ����������� ��� ������� ������� �������������� ������������� (��������, ������������������ ����� ������� �����������, �������������� ���������� �������� �� ������������). ����� ��� ������� ���� ����� ������ ���������� �� ��������� � ������� ��������� ������ ������ � ���������� ������������.
��� ������� ������� ������ ���������� ������� � �������� ���������� �������� ����� ������� �� ��������������� ���������.
������� ������ ���������� �������
1. ��� ������� ��������������� ��������:
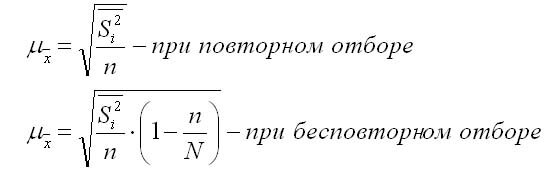
��� S � ������� �� ��������������� ��������� �� ���������� ������������.
2. ��� ���� (��������������� ��������):
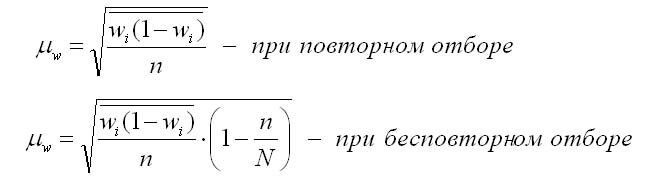
��� w(1 -w) � ��������� - ������� �� ��������������� ��������� ���� (��������������� ��������) �� ���������� ������������.
�������� (���������) �������
� �������� ������� ���������� ��������� ����� �� ����������� ������������ �� ��������� ������, � �� ������������ �����, � ��� ����� � ���� ������� ��� ������� ���� ����������� ����������.
�������� ������� ���������� ���, ��� ������ ������ ��� �� ���������������, �������� ��� ������� �������������, ������������� ��� �������� �������� ������������ ������ ������������ �������� �������� ��������� ����� ��������, ��� �� ���� �������� �������� ����������� ���������� ������.
� ����� � ���, ��� ������ ����� (��� �����) ������������� ��� �������, ������� ������ ������� ��� ������ ������������ ����� ������� ������ �� ������������ (��� �����������) ���������.
������ ������� ������ �������� (���������) �������
1. ��� ������� ��������������� ��������:
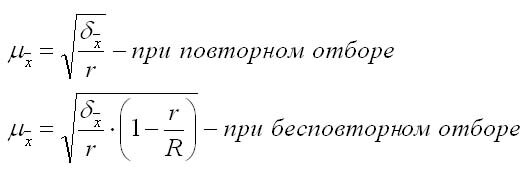
��� r � ����� ���������� �����;
R � ����� ����� �����; ������-������� � ������������ ��������� �������� �������, ������������ �� �������:
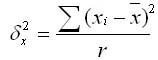
��� xi � ������� i-� �����;
� � ������ ������� �� ���� ���������� ������������.
2. ��� ���� (��������������� ��������):

������������ (�����������) ��������� ���� �������� ������� ������������ �� �������:
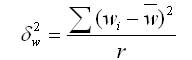
��� w � ���� �������� � i-� �����;
w � ����� ���� �������� �� ���� ���������� ������������.
��������������� �������
��������������� ������� ��������� �������� � �������� ���������� ���������� � ������ ��������� �� �������� � �����. ���� � ��������������� ������� �������������� ������������ � ���������� �������, �� ������� ������ ������������ �� �������:
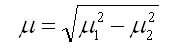
��� �������� � ������� � ������� ������ ������������ � ���������� �������.
��������: �������� B.C. ���������� � �������� � �������: ����. �������. � �.: ��. �����, ���-�� ��������, 2004. � 344 �.


