Предпосылки метода наименьших квадратов

Регрессионный анализ позволяет определить оценки коэффициентов регрессии. Но сами оценки не позволяют сделать вывод, о том, насколько точно эмпирическое уравнение регрессии соответствует уравнению для всей совокупности, насколько близки оценки параметров b₀ и b₁ - коэффициентов к своим теоретическим значениям β₀ и β₁, как близко оцененное значение y_i к условному математическому ожиданию M (Y(X = x_i,), насколько надежны найденные оценки. Для ответа на эти вопросы нужны дополнительные исследования.

Значения y_i зависят от значений x_i и случайных отклонений ε_i. Значит, переменная Y является СВ, напрямую связанной с ε_i . До тех пор, пока не будет определенности в вероятностном поведении ε_i, мы не можем быть уверенными в качестве оценок.

Известно, что для получения по МНК наилучших результатов требуется, чтобы выполнялся ряд предпосылок относительно случайного отклонения.

См. также теорему Маркова-Гаусса.

Предпосылки МНК (условия Гаусса-Маркова)

Математическое ожидание случайного отклонения е_i равно нулю: M(е_i) = 0 для всех наблюдений.

Данное условие означает, что случайное отклонение в среднем не оказывает влияния на зависимую переменную. В определенном наблюдении случайный член может быть положительным или отрицательным, но он не должен иметь систематического смещения. Выполнимость M(е_i) = 0 влечет выполнимость:
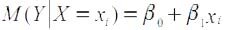
Дисперсия случайных отклонений epsiloni постоянна: D(εi) = D (εj ) = σ² = const для любых наблюдений i и j.

Условие независимости дисперсии ошибки от номера наблюдения называется гомоскедастичностью (homoscedasticity). Невыполнимость этой предпосылки называется гетероскедастичностью (heteroscedasticity).

Поскольку D(ε)=M((εj - Mεj))² = M(ε²), то эту предпосылку можно переписать в форме: M(е²_i) = σ². Причины невыполнимости данной предпосылки и проблемы, связанные с этим, подробно рассматриваются ниже.
Случайные отклонения εi и εj являются независимыми друг от друга для i ≠ j.

Выполнимость этой предпосылки предполагает, что отсутствует систематическая связь между любыми случайными отклонениями. Величина и определенный знак любого случайного отклонения не должны быть причинами величины и знака любого другого отклонения.

Выполнимость данной предпосылки влечет следующее соотношение:

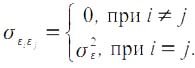
Если данное условие выполняется, то можно говорить об отсутствии автокорреляции. С учетом выполнимости предпосылки 1 данное соотношение можно переписать в виде:

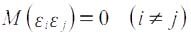
Причины невыполнимости этой предпосылки и проблемы, связанные с ними, рассматриваются ниже.
Случайное отклонение должно быть независимо от объясняющих переменных.

Обычно это условие выполняется автоматически, если объясняющие переменные не являются случайными в модели.

Данное условие предполагает выполнимость следующего соотношения:

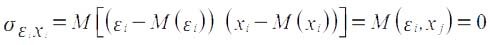
Заметим, что выполнимость этой предпосылки не столь критична для эконометрических моделей.
Модель является линейной относительно параметров.

Для случая множественной линейной регрессии существенными являются еще две предпосылки.
Отсутствие мультиколлинеарности.

Между объясняющими переменными отсутствует сильная линейная зависимость.
Случайные отклонения εi, i = 1, 2, ... , n, имеют нормальное распределение.

Выполнимость данной предпосылки важна для проверки статистических гипотез и построения интервальных оценок.

Наряду с выполнимостью указанных предпосылок при построении классических линейных регрессионных моделей делаются еще некоторые предположения. Например:

объясняющие переменные не являются случайными величинами;
число наблюдений намного больше числа объясняющих переменных (числа факторов уравнения);
отсутствуют ошибки спецификации, т. е. правильно выбран вид уравнения и в него включены все необходимые переменные.

Зачастую полагают, что число наблюдений должно быть как минимум в 5-6 раз больше числа параметров уравнения (числа объясняющих переменных).

Задачи по эконометрике на предпосылки МНК решаются тут