
Тест Парка
Предполагается, что дисперсия σ2 является функцией i-го значения объясняющей переменной. Р. Парк предложил следующую функциональную зависимость:
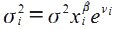
Прологарифмировав, получим:
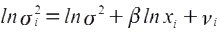
Так как дисперсии σ2 обычно неизвестны, то их заменяют оценками квадратов отклонений e2.
Критерий Парка включает следующие этапы:
- Строится уравнение регрессии: yi = b0 + b1xi + ei.
- Для каждого наблюдения определяются
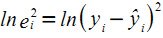
- Оцениваются коэффициенты регрессии:
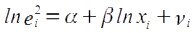
- Проверяется статистическая значимость коэффициента b (оценки β) на основе t-статистики t = b/Sb. Если коэффициент b (β) статистически значим, то это означает наличие связи между lne2 и lnx, т.е. гетероскедастичности в эконометрических данных.
Использование в критерии Парка конкретной функциональной зависимости может привести к необоснованным выводам (например, коэффициент β статистически незначим, а гетероскедастичность имеет место). Возможна еще одна проблема. Для случайного отклонения vi в свою очередь может иметь место гетероскедастичность. Поэтому критерий Парка дополняется другими тестами.


